Il y a quelques mois, François LUCQUET et Anaïs ETIENNE nous faisaient part[1] de l’intérêt croissant pour la quantification des risques cyber, mais nous mettaient également en garde contre un trop grand empressement à s’engager sur la voie de la quantification sans réflexion préalable. Leur analyse, toujours d’actualité, insistait notamment sur le niveau de maturité requis pour s’engager dans une méthode d’estimation quantitative, ce dernier point réduisant drastiquement le périmètre des organisations susceptibles de s’engager sur cette voie. Pourtant, certaines méthodes de quantification sont à l’origine de solutions qui redonnent espoir dans la possibilité de chiffrer ses risques en termes financiers, et par la même logique de pouvoir évaluer un retour sur investissement.
Aussi est-il utile à ce point de faire un tour d’horizon des méthodes et théories existantes, ou susceptibles d’aboutir sur des résultats concrets. Dans le big-bang de la quantification du risque cyber, quels sont les ancrages théoriques qui pourraient voir naitre une méthode ? Lesquels ont abouti, lesquels semblent matures ? Pouvons-nous espérer à plus ou moins long terme des alternatives aux méthodes d’évaluation quantitatives actuelles ?
Feuille de route : Analyse de risque et quantification : qu’en attendre ?
Pour situer la quantification dans le champ de la gestion du risque, commençons par préciser ce que nous cherchons. Au sein d’un procédé de gestion de risque, l’objectif est avant tout de définir une valeur chiffrée exploitable illustrant un niveau de risque (généralement un coût financier).
Il s’agit donc, en reprenant les termes de l’ISO 27k, uniquement d’une nouvelle évaluation du risque. En effet, les phases précédentes de contextualisation et d’identification des risques n’ont pas à priori de raisons d’être concernées par la quantification. Les phases de traitement, d’acceptation, de supervision ou de communication du risque, si elles bénéficieront des résultats de l’analyse quantitative, n’ont pas plus vocation à être bousculées dans leurs fondements. Il s’agit donc en réalité de trouver des moyens pour estimer chaque risque.
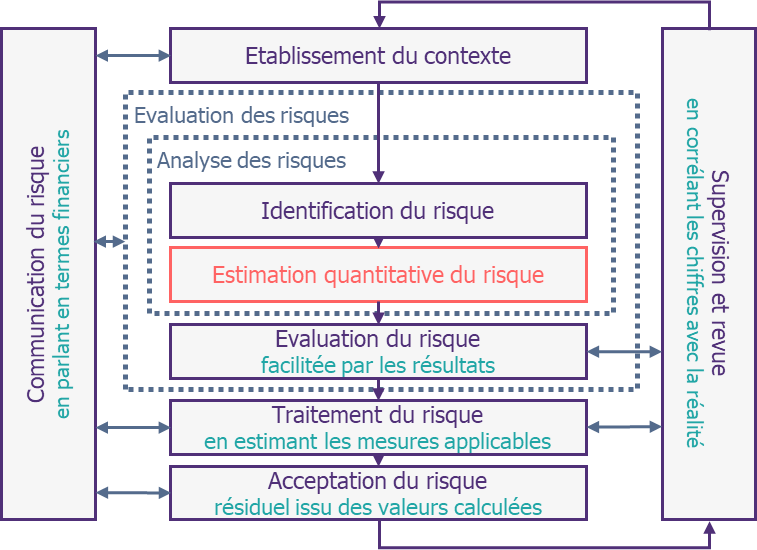
Ce point, plutôt trivial mais crucial, nous permet de nous assurer que, bien que fondamentalement différentes des méthodes qualitatives dans leurs résultats, les méthodes quantitatives s’adosseront quoi qu’il en soit à des méthodes préexistantes. Ceci permet de se rassurer sur le fait que, bien qu’il soit nécessaire pour les employer de disposer d’une gestion de risque mature, cette gestion de risque sera également le socle de la quantification (qui exploitera ainsi la phase d’identification préexistante).
Maintenant que nous avons cadré l’apport de la quantification dans l’analyse globale des risques d’une organisation, précisons ce que nous souhaitons en attendre indépendamment de la possibilité de réalisation de ces assertions :
- D’une part, il est impératif que cette méthode soit plus précise dans son résultat par rapport à la méthode qualitative qui la précède. Ceci signifie surtout que, dès la première occurrence et sans avoir fourni de résultat auparavant, elle doit donner une estimation chiffrée précise (qui peut dans la mesure du possible contenir plusieurs valeurs : risque maximal ou risque probable notamment).
- Nous pouvons également vouloir qu’elle soit plus rapide à réaliser, ou du moins qu’elle se réalise dans un temps acceptable, afin de pouvoir remplacer complètement à terme l’estimation qualitative. Il s’agit ici du temps qu’il serait nécessaire pour mettre en œuvre l’analyse, et ce sans avoir à s’inquiéter outre mesure des délais du calcul (ce dernier pouvant aujourd’hui assez efficacement être délégué, en particulier via le cloud). Il s’agit finalement si nous croisons ce souhait avec le précédent d’avoir une meilleure efficience que l’évaluation qualitative.
- Par ailleurs, il est souhaitable que l’estimation quantitative s’appuie sur des données concrètes, afin de gagner en crédibilité dans les résultats produits. En effet, le processus d’une méthode quantitative étant fondée sur des théories mathématiques, seule une implémentation incorrecte pourrait introduire de la subjectivité dans les valeurs obtenues. Ce dernier point permettrait de justifier qu’en un temps équivalent à l’analyse qualitative, nous ayons des résultats plus fins.
- Enfin, et cela découle du point précédent, il nous est nécessaire de disposer d’une taxonomie précise, afin que les données à collecter soient clairement définies quel que soit le risque envisagé. En effet, si l’estimation quantitative s’appuie sur des théories mathématiques éprouvées, la qualité des données produites ne dépendra alors plus que de la qualité des données utilisées en entrée, et plus particulièrement de la pertinence et de la cohérence de la donnée au vue de sa définition.
Au centre de la galaxie : passer de la théorie à la pratique
Ayant précisé quels sont les caractéristiques de la quantification, voyons maintenant quels sont les théories mathématiques qui permettraient de prendre en compte l’aléa lié à un risque.
Considérons par exemple la théorie des Fuzzy sets, ou ensembles flous. Cette théorie mathématique est basée sur le principe qu’un élément, au lieu d’appartenir ou non à un ensemble, puisse ne lui appartenir que partiellement selon un degré variable. Cela pourrait permettre de faire ressortir l’occurrence ou l’impact d’un risque au travers du degré d’appartenance de ce risque à des ensembles. Cette théorie, bien qu’intéressante, n’a cependant pas débouché sur des applications concrètes.
Une autre approche, que l’on pourrait qualifier de corrélative, reposerait sur l’utilisation de réseaux de neurones auto-apprenants pour déterminer à partir de données de CTI, quel serait le niveau du risque d’une entreprise au vu de ses caractéristiques. Cette théorie a bénéficié de l’engouement actuel pour l’intelligence artificielle, au point de déboucher au niveau universitaire sur des études comparant les différents modes d’apprentissage (notamment BP[2] ou RBF[3]) en vue d’une utilisation dans le cadre d’une analyse de risque cyber. Cependant, elle ne semble pas à ce jour suffisamment mature pour parvenir à obtenir une méthode réaliste.
Finalement, la seule solution mathématique ayant porté des fruits à ce jour a été l’analyse statistique (et la théorie des jeux qui offre le moyen de combiner les distributions statistiques, voir à ce sujet le billet « Quantification du risque et données : conseils et outils »[4]). Le principe de l’analyse statistique est de se baser sur des observations statistiques pour estimer le niveau d’un risque. L’aléa du risque est alors, en grande partie, pris en compte par la répartition de la distribution statistique.
A partir de ces statistiques, deux approches sont envisageables :
- La première est illustrée par une méthode proposée par l’IMF[5]. Elle se propose d’évaluer un risque cyber par une analyse statistique fine et détaillée. Elle est cependant très calculatoire et peu accessible pour une utilisation régulière dans le cadre d’une estimation quantifiée du risque. Elle garde cependant un intérêt indubitable dans le cadre d’une analyse d’un niveau de risque cyber sur plusieurs entités dont on disposerait de données, ce qui peut s’avérer utile pour un assureur ou dans le milieu de la banque. Elle reste cependant cloisonnée à cette utilisation. Réduisant d’autant le périmètre déjà limité des entités disposant d’une maturité cyber acceptable, cette méthode ne semble pas pouvoir proposer à court ou moyen terme une solution exploitable à l’échelle du SI d’une organisation.
- La seconde consiste à décomposer tout risque cyber en fonction de caractéristiques communes. C’est notamment l’approche de la méthodologie FAIR : elle propose dans sa taxonomie (cf. ‘comment appliquer la méthode FAIR’1) une dissociation du risque en fonction de son occurrence et de l’impact estimé d’un point de vue financier. FAIR propose ensuite une déclinaison de ces deux paramètres qui, du fait de leur caractère universel, peuvent s’appliquer de ce fait à n’importe quel risque cyber. Ce type de méthode a donc l’avantage de proposer un processus identique pour l’analyse de tout risque cyber, favorisant son utilisation dans un contexte organisationnel qui peut ensuite comparer des risques cyber de nature distincte.
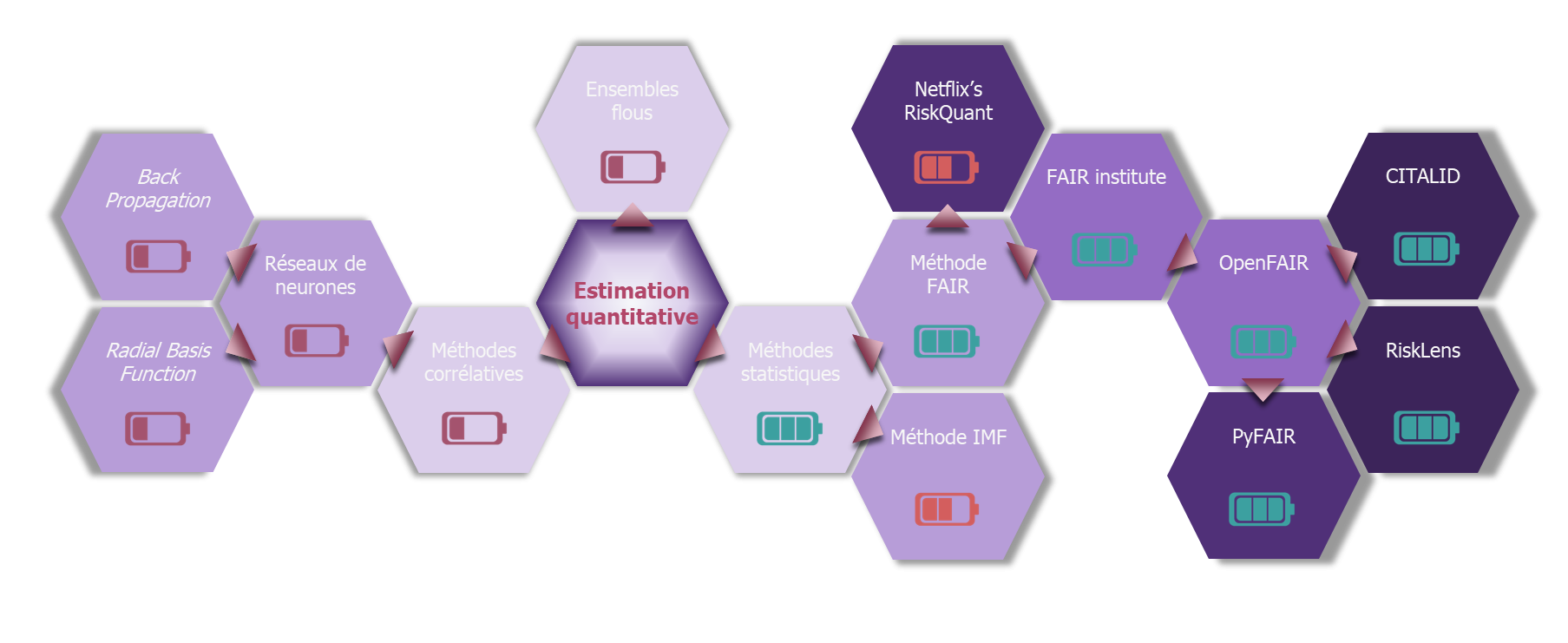
La galaxie de la quantification
La méthode FAIR : un trou noir supermassif
Actuellement, seule la méthode FAIR a donné naissance à des solutions de quantification exploitables au sein d’une entreprise. Son monopole dans le domaine est tel, qu’elle est devenue une référence incontournable pour qu’une solution ou une méthodologie subsiste. Tel un trou noir, elle attire à elle toutes les solutions actuelles de quantification. Nous pouvons par exemple pour illustrer ceci citer la bibliothèque Risquant, développée par le département R&D de Netflix[6]. Cette dernière annonce clairement s’appuyer sur la méthode FAIR. Elle prend néanmoins une grande liberté dans l’interprétation de la taxonomie et de l’analyse, mais le fait de citer cette filiation lui permet cependant d’être plus facilement acceptée et reconnue.
Cette hégémonie de FAIR s’explique assez facilement :
- Pour commencer, c’est une méthode pragmatique par conception. Son inventeur, Jack Jones, l’a mise sur pied alors qu’il était RSSI d’un grand groupe américain, et qu’il lui était demandé de justifier du ROI cyber. Elle a donc été initiée dans un but opérationnel, puis s’est affinée et a gagné en crédibilité en s’appuyant sur des outils et des théories mathématiques. Ce concept de développement (i.e. le fait que la méthode soit née d’un besoin puis justifiée ensuite mathématiquement), fait de FAIR une méthode particulièrement appréciée des premiers concernés que sont les RSSI et autres cyber-risk managers.
- Ensuite, elle a été particulièrement visionnaire, puisqu’elle a précédé toutes les autres méthodes. Apparue en 2001, elle a fait dès 2006 l’objet d’une publication explicitant en détail son fonctionnement et sa taxonomie. Au fur et à mesure, une communauté s’est constituée autour de Jack Jones et de sa méthode, le FAIR Institute. Ce dernier a eu à cœur de poursuivre la maturation et la diffusion de la méthode. Ceci s’est notamment concrétisé par la mise en place de facilitateurs pour la rendre toujours plus efficiente et exploitable.
- La méthode FAIR dispose également d’une base particulièrement solide : outre la publication évoquée ci-dessus et qui a fait l’objet en 2016 d’une réédition enrichie, elle s’appuie sur deux documents de standardisation, édités par l’OpenGroup (consortium à l’origine du standard d’architecture de SI TOGAF). L’OpenGroup propose également une certification à la méthode, basée sur ces deux standards, et qui ajoutent au rayonnement de la méthode.
- Enfin, FAIR est fortement soutenue (en particulier outre-Atlantique) : la communauté qui l’anime est particulièrement active et contribue autant à son évolution qu’à sa promotion : les liens entre l’OpenFAIR et le FAIR Institute, tous deux cités ci-dessus, sont sensiblement étroits. La solidité de ses liens est assurée par le fait que Jack Jones, père de la méthode, joue un rôle central dans les deux organisations.
Ainsi, dans le monde de la quantification du risque cyber, les seules solutions opérationnelles à ce jour s’appuient toutes, avec une filiation plus ou moins grande mais toujours affichée, sur la méthodologie FAIR.
Si la maturité de celle-ci semble désormais acquise, son monopole dans le domaine permet avec peu de doute d’envisager, au moins pour les années à venir, qu’elle restera la seule méthode de quantification. Pour qu’une autre méthode puisse un jour faire jeu égal, et outre le fait qu’il lui faudra asseoir sa crédibilité conceptuelle, il lui faudra surtout se faire une place à côté de l’hégémonie de FAIR, tout en prouvant qu’elle est plus efficiente que cette dernière, qui a désormais acquis ses lettres de noblesse.
[1] https://www.riskinsight-wavestone.com/2020/06/la-quantification-du-risque-cybersecurite/
[2] Back-propagation : propagation inverse
[3] Radial basis functions : fonctions de base radiale
[4] Article 2 disponible sur Risk Insight
[5] https://www.imf.org/en/Publications/WP/Issues/2018/06/22/Cyber-Risk-for-the-Financial-Sector-A-Framework-for-Quantitative-Assessment-45924
[6] https://netflixtechblog.com/open-sourcing-riskquant-a-library-for-quantifying-risk-6720cc1e4968


